Algorithm Analysis

1. What Is Algorithm Analysis?

2. Big O Notation

3. Example: Anagram Detection

4. Benchmark of Python Data Structures: Lists/Dictionaries

2.1~2.2 What Is Algorithm Analysis?

An interesting question often arises. When two programs solve the same problem but look different, is one program better than the other?

In order to answer this question, we need to remember that there is an important difference between a program and the underlying algorithm that the program is representing!

There may be many programs for the same algorithm, depending on the programmer and the programming language being used!

To explore this difference further, consider the function that computes the sum of the first $n$ integers. The algorithm uses the idea of an accumulator variable that is initialized to 0. The solution then iterates through the $n$ integers, adding each to the accumulator.

def sum_of_n(n):
    the_sum = 0
    for i in range(1, n + 1):
        the_sum = the_sum + i
    return the_sum

print(sum_of_n(10))

55

Now look at the function below:

def foo(tom):
    fred = 0
    for bill in range(1, tom + 1):
        barney = bill
        fred = fred + barney
    return fred

print(foo(10))

55

At first glance it may look strange, but this function is essentially doing the same thing as the previous one. Here, we did not use good identifiers for readability, and we used an extra assignment statement that was not really necessary!

The function sum_of_n() is certainly better than the function foo() if you are concerned with readability. Easy to read and easy to understand is important for beginner. In this course, however, we are also interested in characterizing the algorithm itself.

Algorithm analysis is concerned with comparing algorithms based upon the amount of computing resources that each algorithm uses.

We want to be able to consider two algorithms and say that one is better than the other because it is more efficient in its use of those resources or perhaps because it simply uses fewer.

There are two different ways to look at this. One way is to consider the amount of space or memory an algorithm requires to solve the problem.

As an alternative to space requirements, we can analyze and compare algorithms based on the amount of time they require to execute.

One way is that we can measure the execution time for the function sum_of_n() to do a benchmark analysis. In Python, we can benchmark a function by noting the starting time and ending time within the system we are using.

import time

def sum_of_n_2(n):
    start = time.time()
    the_sum = 0
    for i in range(1, n + 1):
        the_sum = the_sum + i
    end = time.time()
    return the_sum, end - start

for i in range(5):
    print("Sum is %d required %10.7f seconds" % sum_of_n_2(100_000))

Sum is 5000050000 required  0.0040004 seconds
Sum is 5000050000 required  0.0029991 seconds
Sum is 5000050000 required  0.0040011 seconds
Sum is 5000050000 required  0.0039995 seconds
Sum is 5000050000 required  0.0030422 seconds

We discover that the time is fairly consistent. What if we run the function adding the first 1,000,000 integers?

for i in range(5):
    print("Sum is %d required %10.7f seconds" % sum_of_n_2(1_000_000))

Sum is 500000500000 required  0.0360823 seconds
Sum is 500000500000 required  0.0369999 seconds
Sum is 500000500000 required  0.0349967 seconds
Sum is 500000500000 required  0.0359645 seconds
Sum is 500000500000 required  0.0359993 seconds

Now consider the following function, which shows a different means of solving the summation problem. This function takes advantage of a closed equation $\sum_{i=1}^{n} i = \frac {(n)(n+1)}{2}$ to compute the sum of the first $n$ integers without iterating.

def sum_of_n_3(n):
    start = time.time()
    the_sum = (n * (n + 1)) // 2
    end = time.time()
    return the_sum, end - start
print(sum_of_n_3(10)[0])

55

If we do the same benchmark measurement for sum_of_n_3(), using four different values for $n$ (100,000, 1,000,000, 10,000,000, and 100,000,000), we get the following results:

print("Sum is %d required %10.7f seconds" % sum_of_n_3(100_000))
print("Sum is %d required %10.7f seconds" % sum_of_n_3(1_000_000))
print("Sum is %d required %10.7f seconds" % sum_of_n_3(10_000_000))
print("Sum is %d required %10.7f seconds" % sum_of_n_3(100_000_000))

Sum is 5000050000 required  0.0000000 seconds
Sum is 500000500000 required  0.0000000 seconds
Sum is 50000005000000 required  0.0000000 seconds
Sum is 5000000050000000 required  0.0000000 seconds

First, the times recorded above are shorter than any of the previous examples. Second, they are very consistent no matter what the value of $n$. It appears that sum_of_n_3() is hardly impacted by the number of integers being added.

Intuitively, we can see that the iterative solutions seem to be doing more work since some program steps are being repeated. Also, the time required for the iterative solution seems to increase as we increase the value of $n$.

However, if we ran the same function on a different computer or used a different programming language, we would likely get different results. It could take even longer to perform sum_of_n_3() if the computer were older.

We need a better way to characterize these algorithms with respect to execution time. The benchmark does not really provide us with a useful measurement because it is dependent on a particular machine, program, time of day, compiler, and programming language.

We would like to have a characterization that is independent of the program or computer being used. This measure would then be useful for judging the algorithm alone and could be used to compare algorithms across implementations!

2.3 Big O Notation

If each of these steps is considered to be a basic unit of computation, then the execution time for an algorithm can be expressed as the number of steps required to solve the problem!

Deciding on an appropriate basic unit of computation can be a complicated problem and will depend on how the algorithm is implemented.

A good basic unit of computation for comparing the summation algorithms might be the number of assignment statements performed to compute the sum.

In the function sum_of_n():

def sum_of_n(n):
    the_sum = 0
    for i in range(1, n + 1):
        the_sum = the_sum + i
    return the_sum

The number of assignment statements is 1 (the_sum = 0) plus the value of $n$ (the number of times we perform the_sum = the_sum + 1). We can denote this by a function, call it $T$, where $T(n)= n+1$.

The parameter $n$ is often referred to as the size of the problem, and we can read this as $T(n)$ is the time it takes to solve a problem of size $n$, namely $n+1$ steps.

We can then say that the sum of the first 100,000 integers is a bigger instance of the summation problem than the sum of the first 1,000. Our goal then is to show how the algorithm’s execution time (steps) changes with respect to the size of the problem.

It turns out that the exact number of operations is not as important as determining the most dominant part of the function. In other words, as the problem gets larger, some portion of the function tends to overpower the rest.

The order of the magnitude of the function describes the part of $T(n)$ that increases the fastest as the value of $n$ increases. Order of magnitude is often called Big O notation (for order) and written as $O(f(n))$.

It provides a useful approximation of the actual number of steps in the computation. The function $f(n)$ provides a simple representation of the dominant part of the original $T(n)$.

In the above example, $T(n)=n+1$. As $n$ gets larger, the constant 1 will become less and less significant to the final result. If we are looking for an approximation for $T(n)$, then we can drop the 1 and simply say that the running time is $O(n)$.

It is important to note that the 1 is certainly significant for $T(n)$. However, as $n$ gets large, our approximation will be just as accurate without it.

As another example, suppose that for some algorithm, the exact number of steps is $T(n)=5n^2+27n+1005$. When $n$ is small, say 1 or 2, the constant 1005 seems to be the dominant part of the function. However, as $n$ gets larger, the $n^2$ term becomes the most important! .

In fact, when $n$ is really large, the other two terms become insignificant for the final result. Again, to approximate $T(n)$ as $n$ gets large, we can ignore the other terms and focus on $5n^2$.

In addition, the coefficient $5$ becomes insignificant as $n$ gets large. We would say then that the function $T(n)$ has an order of magnitude $f(n)=n^2$, or simply that it is $O(n^2)$.

Sometimes the performance of an algorithm depends on the exact values of the data rather than simply the size of the problem. For these kinds of algorithms we need to characterize their performance in terms of best-case, worst-case, or average-case performance.

The worst-case performance refers to a particular data set where the algorithm performs especially poorly, whereas a different data set for the exact same algorithm might have extraordinarily good (best-case) performance.

However, in most cases the algorithm performs somewhere in between these two extremes (average-case performance).

A number of very common order of magnitude functions will come up over and over as you study algorithms:

f(n)	Name
1	Constant
log(n)	Logarithmic
n	Linear
n log(n)	Log linear
n2	Quadratic
n3	Cubic
2n	Exponential

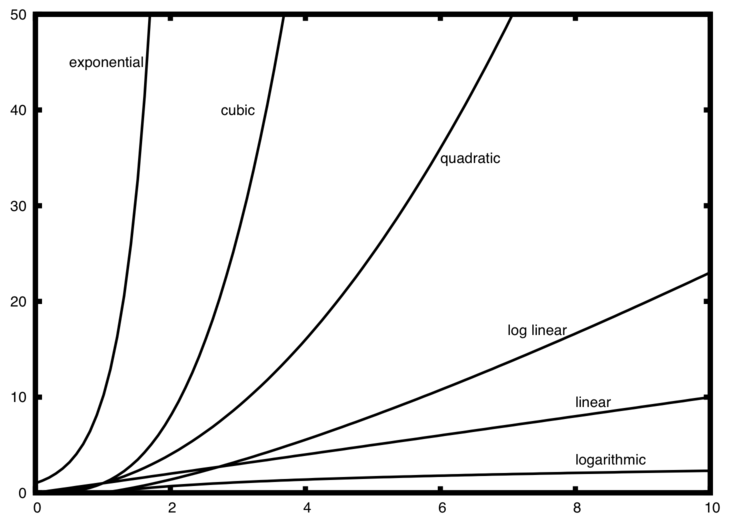
Notice that when $n$ is small, the functions are not very well defined with respect to one another. It is hard to tell which is dominant.

As a final example, suppose that we have the fragment of Python code:

n = 100
# Start of the code
a = 5
b = 6
c = 10
for i in range(n):
    for j in range(n):
        x = i * i
        y = j * j
        z = i * j
for k in range(n):
    w = a * k + 45
    v = b * b
d = 33

• The first part is the constant 3, representing the three assignment statements at the start of the fragment.
• The second part is $3n^2$ due to the nested iteration.
• The third part is $2n$ and the fourth part is the constant 1, representing the final assignment statement.

This gives us $T(n)=3+3n^2+2n+1=3n^2+2n+4$. We can see that the $n^2$ term will be dominant and therefore this code is $O(n^2)$. All of the other terms as well as the coefficient on the dominant term can be ignored as $n$ grows larger!

Exercise: Analyze the time complexity of the following code (You can consider $n$ as the power of 2 for approximation):

i = 1
while i <= n:
    for j in range(1, i + 1):
        x += 1
    i *= 2

Ans:

2.4 An Anagram Detection Example

A good example problem for showing algorithms with different orders of magnitude is the classic anagram detection problem for strings. One string is an anagram of another if the second is simply a rearrangement of the first. For example, "heart" and "earth" are anagrams. The strings "python" and "typhon" are anagrams as well!

For the sake of simplicity, we will assume that the two strings in question are of equal length and that they are made up of symbols from the set of 26 lowercase alphabetic characters.

Our goal is to write a boolean function that will take two strings and return whether they are anagrams.

2.4.1 Solution 1: Anagram Detection Checking Off

Our first solution to the anagram problem will:

1. Check the lengths of the strings

2. Check to see that each character in the first string actually occurs in the second. If it is possible to check off each character, then the two strings must be anagrams.

Checking off a character will be accomplished by replacing it with the special value None. However, since strings in Python are immutable, the first step will be to convert the second string to a list. Each character from the first string can be checked against the characters in the list and if found, checked off by None.

def anagram_solution_1(s1, s2):
    still_ok = True
    if len(s1) != len(s2): # Step1
        still_ok = False

    a_list = list(s2)
    pos_1 = 0
    i = 0
    while pos_1 < len(s1) and still_ok: # Step2
        pos_2 = 0
        found = False
        while pos_2 < len(a_list) and not found:
            if s1[pos_1] == a_list[pos_2]:
                found = True
            else:
                pos_2 = pos_2 + 1
            i = i+1
        if found:
            del a_list[pos_2] 
        else:
            still_ok = False
        pos_1 = pos_1 + 1

    return still_ok, i

print(anagram_solution_1("apple", "pleap"))  # expected: True
print(anagram_solution_1("abcd", "dcba"))  # expected: True
print(anagram_solution_1("abcd", "dcda"))  # expected: False

(True, 10)
(True, 10)
(False, 7)

Each of the $n$ characters in s1 will cause an iteration through up to $n$ characters in the list from s2. Each of the $n$ positions in the list will be visited once to match a character from s1. The number of visits then becomes the sum of the integers from 1 to $n$. Therfore, $\sum_{i=1}^{n} i = \frac {n(n+1)}{2}$!

As $n$ gets large, the $n^2$ term will dominate. Therefore, this solution is $O(n^2)$.

2.4.2 Solution 2: Sort and Compare

Another solution to the anagram problem will make use of the fact that even though s1 and s2 are different, they are anagrams only if they consist of exactly the same characters.

So if we begin by sorting each string alphabetically from a to z, we will end up with the same string if the original two strings are anagrams!

def anagram_solution_2(s1, s2):
    a_list_1 = list(s1)
    a_list_2 = list(s2)

    a_list_1.sort()
    a_list_2.sort()

    return a_list_1 == a_list_2, a_list_1, a_list_2

print(anagram_solution_2("apple", "pleap"))  # expected: True
print(anagram_solution_2("abcd", "dcba"))  # expected: True
print(anagram_solution_2("abcd", "dcda"))  # expected: False

(True, ['a', 'e', 'l', 'p', 'p'], ['a', 'e', 'l', 'p', 'p'])
(True, ['a', 'b', 'c', 'd'], ['a', 'b', 'c', 'd'])
(False, ['a', 'b', 'c', 'd'], ['a', 'c', 'd', 'd'])

At first glance you may be tempted to think that this algorithm is $O(n)$, since there is one simple iteration to compare the $n$ characters after the sorting process. However, the two calls to the Python sort() method are not without their own cost. As we will see in Chapter 5, sorting is typically either $O(n^2)$ or $O(n\log n)$, so the sorting operations dominate the iteration.

2.4.3 Solution 3: Brute Force

A brute force technique for solving a problem tries to exhaust all possibilities. For the anagram detection problem, we can simply generate a list of all possible strings using the characters from s1 and then see if s2 occurs.

However, when generating all possible strings from s1, there are $n$ possible first characters, $n-1$ possible characters for the second position, and so on. The total number of candidate strings is $n!$. Although some of the strings may be duplicates, the program cannot know this ahead of time!

It turns out that $n!$ grows even faster than $2^n$ as $n$ gets large. In fact, if s1 were 20 characters long, there would be $20! = 2,432,902,008,176,640,000$ possible candidate strings. If we processed one possibility every second, it would still take us $77,146,816,596$ years to go through the entire list!

2.4.4 Solution 4: Count and Compare

Our final solution to the anagram problem takes advantage of the fact that any two anagrams will have the same number of a’s, the same number of b’s, the same number of c’s, and so on.

In order to decide whether two strings are anagrams

1. First count the number of times each character occurs. Since there are 26 possible characters, we can use a list of 26 counters, one for each possible character. Each time we see a particular character, we will increment the counter at that position.

2. In the end, if the two lists of counters are identical, the strings must be anagrams!

def anagram_solution_4(s1, s2):
    c1 = [0] * 26 # Step 1, use ASCII code
    c2 = [0] * 26

    for i in range(len(s1)):
        pos = ord(s1[i]) - ord("a")
        c1[pos] = c1[pos] + 1

    for i in range(len(s2)):
        pos = ord(s2[i]) - ord("a")
        c2[pos] = c2[pos] + 1

    return c1 == c2, c1, c2

print(anagram_solution_4("apple", "pleap"))  # expected: True
print(anagram_solution_4("abcd", "dcba"))  # expected: True
print(anagram_solution_4("abcd", "dcda"))  # expected: False

(True, [1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
(True, [1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
(False, [1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

Unlike the first solution, none of the loops are nested. The first two iterations used to count the characters are both based on $n$. The third iteration, comparing the two lists of counts, always takes 26 steps since there are 26 possible characters in the strings. Adding it all up gives us $T(n)=2n+26$ steps. That is $O(n)$. We have found a linear order of magnitude algorithm for solving this problem!

Before leaving this example, we need to say something about space requirements. Although the last solution was able to run in linear time, it could only do so by using additional storage to keep the two lists of character counts. In other words, this algorithm sacrificed space in order to gain time.

On many occasions you will need to make decisions between time and space trade-offs. In this case, the amount of extra space is not significant. However, if the underlying alphabet had millions of characters, there would be more concern.

2.6 Performance of Python Data Structures: Lists

Python had many choices to make when they implemented the list data structure. To help them make the right choices they looked at the ways that people would most commonly use the list, and they optimized their implementation of a list so that the most common operations were very fast!

Of course they also tried to make the less common operations fast, but when a trade-off had to be made the performance of a less common operation was often sacrificed in favor of the more common operation.

Two common operations are indexing and assigning to an index position. Both of these operations take the same amount of time no matter how large the list becomes. When an operation like this is independent of the size of the list, it is $O(1)$.

Another very common programming task is to grow a list. You can use the append() method or the concatenation operator. The append() method is $O(1)$. However, the concatenation operator is $O(k)$, where $k$ is the size of the list that is being concatenated. This is important because it can help you make your own programs more efficient by choosing the right tool for the job.

Let’s look at four different ways we might generate a list of $n$ numbers starting with 0.

1. First we’ll try a for loop and create the list by concatenation
2. We’ll use append() rather than concatenation.

3. Next, we’ll try creating the list using list comprehension
4. using the range() function wrapped by a call to the list constructor.

def test1():
    l = []
    for i in range(1000):
        l = l + [i]

def test2():
    l = []
    for i in range(1000):
        l.append(i)

def test3():
    l = [i for i in range(1000)]

def test4():
    l = list(range(1000))

We will use Python’s timeit module. The module is designed to allow developers to make cross-platform timing measurements by running functions in a consistent environment and using timing mechanisms that are as similar as possible across operating systems!

To use timeit you create a Timer object whose parameters are two Python statements.

1. The first parameter is a Python statement that you want to time
2. The second parameter is a statement that will run once to set up the test.

By default, timeit will try to run the statement one million times. When it’s done it returns the time as a floating-point value representing the total number of seconds.

You can also pass timeit a named parameter called number that allows you to specify how many times the test statement is executed.

from timeit import Timer

t1 = Timer("test1()", "from __main__ import test1")
print(f"concatenation: {t1.timeit(number=1000):15.2f} milliseconds")
t2 = Timer("test2()", "from __main__ import test2")
print(f"appending: {t2.timeit(number=1000):19.2f} milliseconds")
t3 = Timer("test3()", "from __main__ import test3")
print(f"list comprehension: {t3.timeit(number=1000):10.2f} milliseconds")
t4 = Timer("test4()", "from __main__ import test4")
print(f"list range: {t4.timeit(number=1000):18.2f} milliseconds")

concatenation:            1.05 milliseconds
appending:                0.04 milliseconds
list comprehension:       0.02 milliseconds
list range:               0.01 milliseconds

In the experiment above the statement that we are timing is the function call to test1(), test2(), and so on. You are probably very familiar with the from... import statement, but this is usually used at the beginning of a Python program file.

In this case the statement from __main__ import test1 imports the function test1 from the __main__ namespace into the namespace that timeit sets up experiment. The timeit module wants to run the timing tests in an environment that is uncluttered by any variables you may have created that may interfere with your function’s performance in some way!

From the experiment above it is clear that the append() operation is much faster than concatenation. It is interesting to note that the list comprehension is twice as fast as a for loop with an append() operation.

You can look at Table below to see the Big O efficiency of all the basic list operations.

Operation	Big O Efficiency
index []	O(1)
index assignment	O(1)
append()	O(1)
pop()	O(1)
pop(i)	O(n)
insert(i, item)	O(n)
del operator	O(n)
iteration	O(n)
contains (in)	O(n)
get slice [x:y]	O(k)
del slice	O(n)
set slice	O(n+k)
reverse()	O(n)
concatenate	O(k)
sort()	O(n log n)
multiply	O(nk)

You may be wondering about the two different times for pop(). When pop is called on the end of the list it takes $O(1)$, but when pop is called on the first element in the list — or anywhere in the middle — it is $O(n)$.

# we do want to be able to use the list object x in our test
# This approach allows us to time just the single pop statement 
# and get the most accurate measure of the time for that single operation
pop_zero = Timer("x.pop(0)", "from __main__ import x")
pop_end = Timer("x.pop()", "from __main__ import x")

x = list(range(2_000_000))
print(f"pop(0): {pop_zero.timeit(number=1000):10.5f} milliseconds")

x = list(range(2_000_000))
print(f"pop(): {pop_end.timeit(number=1000):11.5f} milliseconds")

pop(0):    0.60367 milliseconds
pop():     0.00004 milliseconds

The above shows one attempt to measure the difference between the two uses of pop(). Popping from the end is much faster than popping from the beginning. However, this does not validate the claim that pop(0) is $O(n)$ while pop() is $O(1)$. To validate that claim we need to look at the performance of both calls over a range of list sizes:

pop_zero = Timer("x.pop(0)", "from __main__ import x")
pop_end = Timer("x.pop()", "from __main__ import x")
print(f"{'n':10s}{'pop(0)':>15s}{'pop()':>15s}")
for i in range(1_000_000, 10_000_001, 1_000_000):
    x = list(range(i))
    pop_zero_t = pop_zero.timeit(number=1000)
    x = list(range(i))
    pop_end_t = pop_end.timeit(number=1000)
    print(f"{i:<10d}{pop_zero_t:>15.5f}{pop_end_t:>15.5f}")

n                  pop(0)          pop()
1000000           0.19326        0.00004
2000000           0.65571        0.00004
3000000           1.14437        0.00004
4000000           1.63495        0.00004
5000000           2.26735        0.00004
6000000           2.86276        0.00004
7000000           3.35547        0.00004
8000000           3.90567        0.00004
9000000           4.50471        0.00004
10000000          4.91603        0.00004

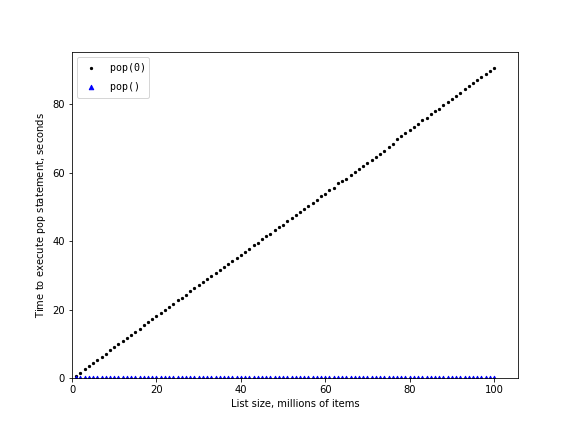
You can see that as the list gets longer and longer the time it takes to pop(0) also increases while the time for pop() stays very flat. This is exactly what we would expect to see for an $O(n)$ and $O(1)$ algorithm!

2.7 Dictionaries

The second major Python data structure is the dictionary. As you probably recall, dictionaries differ from lists in that you can access items in a dictionary by a key rather than a position. Later in this book you will see that there are many ways to implement a dictionary!

The thing that is most important to notice right now is that the get item and set item operations on a dictionary are $O(1)$. Another important dictionary operation is the contains operation. Checking to see whether a key is in the dictionary or not is also $O(1)$. The efficiency of all dictionary operations is summarized in Table below:

Operation	Big O Efficiency
copy	O(n)
get item	O(1)
set item	O(1)
delete item	O(1)
contains (in)	O(1)
iteration	O(n)

One important side note on dictionary performance is that the efficiencies we provide in the table are for amortized worst case performance. In some rare cases the contains, get item, and set item operations can degenerate into $O(n)$ performance, you can refer to Chapter 8 for more information.

For our last performance experiment we will compare the performance of the contains operation between lists and dictionaries. In the process we will confirm that the contains operator for lists is $O(n)$ and the contains operator for dictionaries is $O(1)$.

import timeit
import random

print(f"{'n':10s}{'list':>10s}{'dict':>10s}")
for i in range(100_000, 1_000_001, 100_000):
    t = timeit.Timer(f"random.randrange({i}) in x",
    "from __main__ import random, x")
    x = list(range(i))
    lst_time = t.timeit(number=1000)
    x = {j: None for j in range(i)}
    dict_time = t.timeit(number=1000)
    print(f"{i:<10,}{lst_time:>10.3f}{dict_time:>10.3f}")

n               list      dict
100,000        0.378     0.001
200,000        0.775     0.001
300,000        1.127     0.001
400,000        1.617     0.001
500,000        1.947     0.001
600,000        2.431     0.001
700,000        2.833     0.001
800,000        3.390     0.001
900,000        3.644     0.001
1,000,000      4.186     0.001

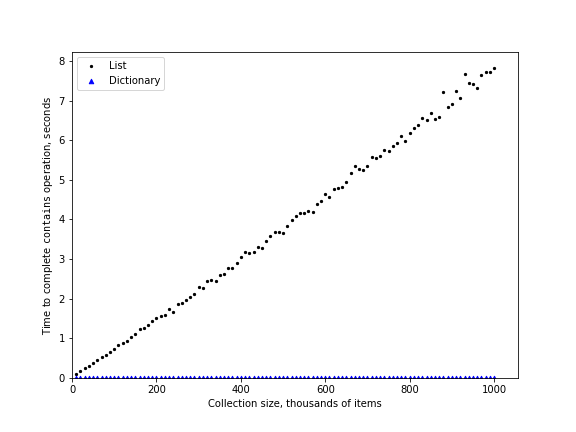
You can see that the dictionary is consistently faster. You can also see that the time it takes for the contains operator on the list grows linearly with the size of the list. This verifies the assertion that the contains operator on a list is $O(n)$. It can also be seen that the time for the contains operator on a dictionary is constant even as the dictionary size grows.

Exercise: Devise an experiment to verify that the list index operator is $O(1)$.

## Your code here

References

1. Textbook CH2